![]() The first item on this page is a link to a problem that was given in a question posted at GSJ Forum. The second link is for a problem that was posted at medium.com. The "arrow diagram" in a more general sense is discussed after the links.
The first item on this page is a link to a problem that was given in a question posted at GSJ Forum. The second link is for a problem that was posted at medium.com. The "arrow diagram" in a more general sense is discussed after the links.
![]() I have taught introductory general chemistry to engineering majors for over 30 years. Upon one occassion, a student commented to me that "I sort of like the homework ... except the booger problems I can't do."
I have taught introductory general chemistry to engineering majors for over 30 years. Upon one occassion, a student commented to me that "I sort of like the homework ... except the booger problems I can't do."![]() But it is exactly these problems, the somewhat more difficult type of problems (the booger problems) that most challenge and encourage students to use their own logical thinking in solving problems. As an example of this sort of problem, with calculations being based on a measured true fact rather than on the erroneously assumed total consumption of the limiting reagent, consider the following problem:
But it is exactly these problems, the somewhat more difficult type of problems (the booger problems) that most challenge and encourage students to use their own logical thinking in solving problems. As an example of this sort of problem, with calculations being based on a measured true fact rather than on the erroneously assumed total consumption of the limiting reagent, consider the following problem:
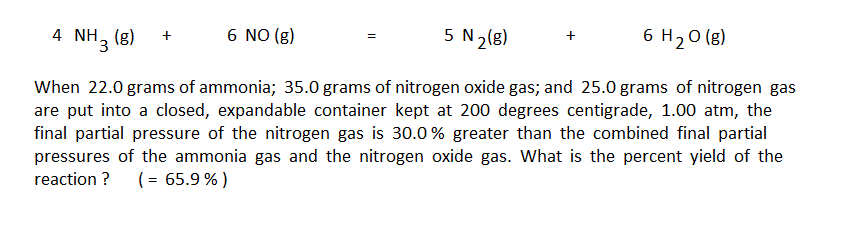
The first step in using the arrow diagram method is to do the conventional unit conversion calculations to convert the masses given in the problem into moles. The preliminary arrow diagram is then set up to represent the moles put in and their change by the reaction:
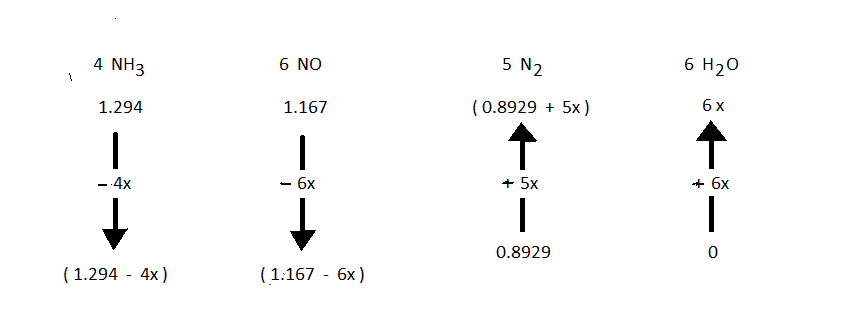
![]() To compute the numerical value of "Xact" (this is the value of "X" for the arrow diagram that corresponds to what actually occurs, with no assumptions) is needed to solve any problem. The symbol "X" with no subscript should be taken to be "Xact". In this particular problem, the given fact about the partial pressues is written as an equation
To compute the numerical value of "Xact" (this is the value of "X" for the arrow diagram that corresponds to what actually occurs, with no assumptions) is needed to solve any problem. The symbol "X" with no subscript should be taken to be "Xact". In this particular problem, the given fact about the partial pressues is written as an equation
![]()
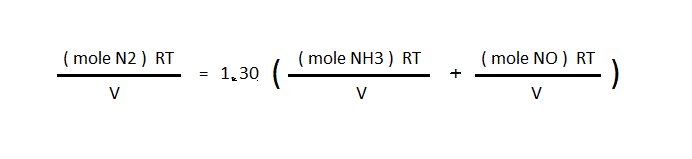
then R, T, and V are cancelled out to leave only the moles of gas
![]() final moles N2 = 1.30( final moles NH3 + final moles NO)
final moles N2 = 1.30( final moles NH3 + final moles NO)
![]() (0.8929 + 5X) = ((1.294 - 4X) + (1.167 - 6X))
(0.8929 + 5X) = ((1.294 - 4X) + (1.167 - 6X))
Solving this equation gives "Xact" = 0.1281
The calculation of "X100" (this being the value of "X" that corresponds to total consumption of the limiting reagent) now gives the easiest way to compute the percent yield of the reaction, this simply being the value of "Xact" divided by the value of "X100" multiplied by 100.
![]()
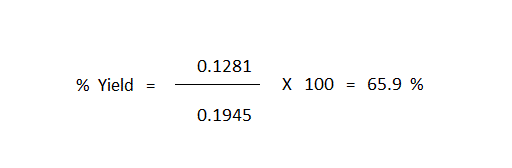
The link below is for a worked out "spaghetti sauce" problem:
The author has written a 70-page paper back booklet titled the "Stoichiometry Problem Solver." This booklet was used by over 2000 students over the course of the authors' teaching career, and it helped most students achieve empowerment over reaction stoichiometry problems. This booklet covers fundamental one-step unit conversions for compounds and for chemical reactions, but it focusses mostly on the arrow diagram method for chemical reactions. If you would like to get a complimentary copy of this booklet, please send a request to the e-mail address below. Include the name ans full mailing address to which the booklet should be sent.
If you have not already seen the other pages posted at this website, you might be interested in at least one of the following:
link link![]() a link to a page the gives a non-relativistic explanation of the Michelson-Morley Experiment.
a link to a page the gives a non-relativistic explanation of the Michelson-Morley Experiment.
linka link that reports possible use of magnets to detect ether drift.