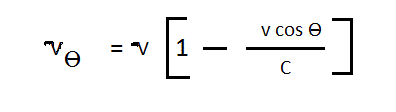
A scientific theory is just an idea made up to logically explain a given set of experimentally observed facts. In some cases, there are two or more ways to explain a given set of facts. In that case, the various explanations need to be compared side-by-side to determine the probably true explanation. The explanation that is the most logical, and the simplest, and that has the least impact on other, unrelated theories, is generally regarded as the explanation most likely to be true.
The Michelson-Morley Experiment of 1887 returned one of the most perplexing facts in the history of science, to wit: a source of light, regardless of its motion, emits light that has the same wavelength in all directions. If the frequency of the emitted light is assumed to be the same in all directions, to get the same wavelength in all directions, the speed at which emitted light propagates away from its source has to be the same in all directions. Most scientists have accepted this relativistic idea as the probably true explanation of the Michelson-Morley Experiment.
But that was without the opportunity to compare the relativistic explanation with a new explanation called "undulatory propagation" (source document: www.jimetherdrift2013.net/etherdrift.html). In this new theory, it is suggested that phase change occurs as an electromagnetic wave propagates. This phase change alters the frequency of the emitted light, so that the frequency of the light emitted at angle theta with the absolute velocity of the source is given by
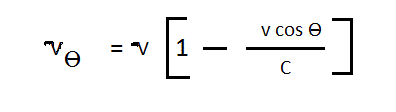
Prior to the Michelson-Morley Experiment, it was thought that emitted light would propagate away from its source at different speeds at different angles, with the speed of light propagating away from the source at angle theta being given by
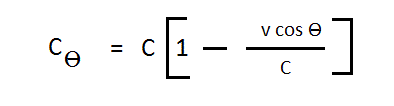
The wavelength of the emitted light, i.e., the speed of propogation divided by the frequency, would then be the same at all angles, just as seen in the Michelson-Morley Experiment.
Any comments of questions about "undulatory propogation" can be sent to the following e-mail address: